每个人都应该去了解人工智能!
本章将用极其简易的知识来介绍人工智能是怎么一回事,保证连初中生都可以看得懂的那种~
按我们门派的规则,每个观点都必须举证,不管观点多么正确,或提出观点的人是谁。
所以接下来,我必须举证:每个人都应该去了解人工智能。
人工智能是怎么来的
人工智能是神经学家、数学家、数学研究生合作的成果:
- 神经学家研究大脑的构成和机制。
- 数学家按神经学家的研究建立模型。
- 会编程的数学研究生实现数学家建立的模型。
这里的数学研究生是指拥有丰富数学知识,并又略懂编程的人。
至于为什么会这么说,下文会讲。
从上面可以看出,人工智能之所以能取得现在的成果,表明了神经科学和数学家的研究结果蛮符合我们大脑的构成和机制。
得出:了解人工智能 就是 了解大脑的构成与机制。
因为:每个人都有大脑
所以:每个人都应该去了解人工智能 = 每个人都应该了解自己大脑构成和机制
举证完毕,谢谢大家。
接着就是如何做到让神经学家和数学家的研究成果,保证连初中生都可以看得懂的那种。
让 数学家 = 小学生
读小学时,我们就会用 2πr 来计算圆的周长,
而 2πr 这条公式是怎么来的,要等我们学了高等数学中的微积分才能推导出来。
然而在应用层面上,无论小学生还是博士生在计算圆的面积的时都是用 2πr 这公式。
而既然谷歌开源了它的人工智能工具 Tensorflow,那么把封装当作信条的程序员,绝对会屏蔽一些极其复杂的东西,让大部分人都可以运用。
《周易·系辞上》:“引而伸之,触类而长之,天下之能事毕矣也。”
《乾》:“六爻发挥,旁通情也。”后以“触类旁通”谓掌握了某一些事物的规律,就能推知同类事物。
所以我将我看到的人工智能知识进行 封装 与 类比,从而保证连初中生都可以看得懂的那种
封装思维还可以用来创业,这里留坑,以后再谈
初中时候的知识
在读初中的时候,我们都解过下面的数学题:
已知方程 y=kx+b,
当 x=6 时,y=15;
当 x=8 时,y=19;求k,b的值(本质是求方程的具体样子)
15=6k+b19=8k+b
用 消元法 解得:k=2;b=3
所以方程是:y=2x+3 (我们得到方程的具体样子,然后提供新 x=5 时,就得到 y=13 )
把上面的描述改变成下面的话,请念三遍,你就明白什么是人工智能了!
定义一方程
y=kx+b
当输入x=6时,y=15
求这方程y=kx+b具体是怎么样的?
定义一方程
y=kx+b
当输入x=6时,y=15
求这方程y=kx+b具体是怎么样的?
定义一方程
y=kx+b
当输入x=6时,y=15
求这方程y=kx+b具体是怎么样的?
特别说明,无论你定义的方程多复杂,都不用你求解方程,不用你解方程,不用你解方程~
你只要像初中数学老师一样,布置作业就好了,而且查作业只说做得好还是做得不好,不用教学生解方程,不用教学生解方程,不用教学生解方程~
由于高中开始,公式方程有个更广泛的称呼:函数,
所以接下来都会用函数的叫法代替方程的叫法,
因此上面的问题也可以用下面函数表示法来表述问题。
当 f(6) = 15
当 f(8) = 19
求 f = ?; 这个 f 函数是怎么样的?
答 f 这个函数的形式是:y = 2x+3
数学家的建模
神经学家现代机器扫描人的大脑,得:
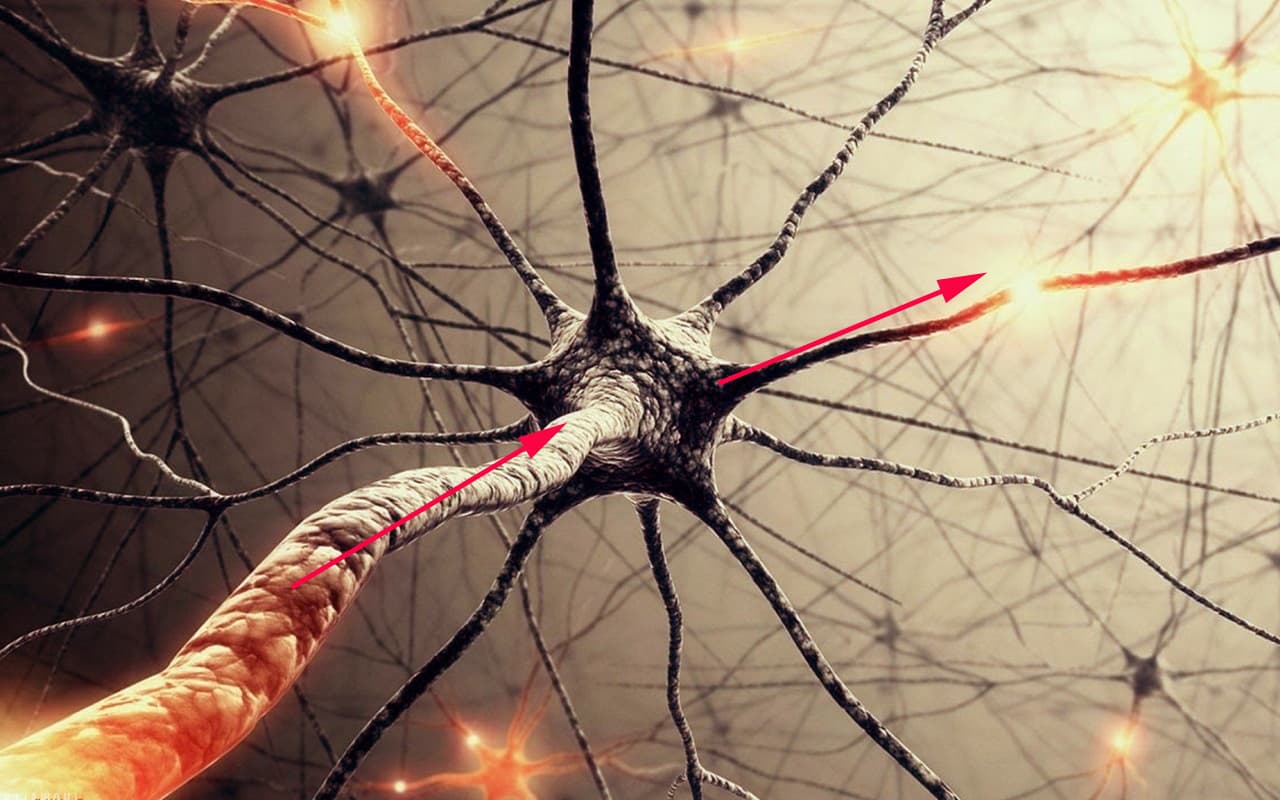
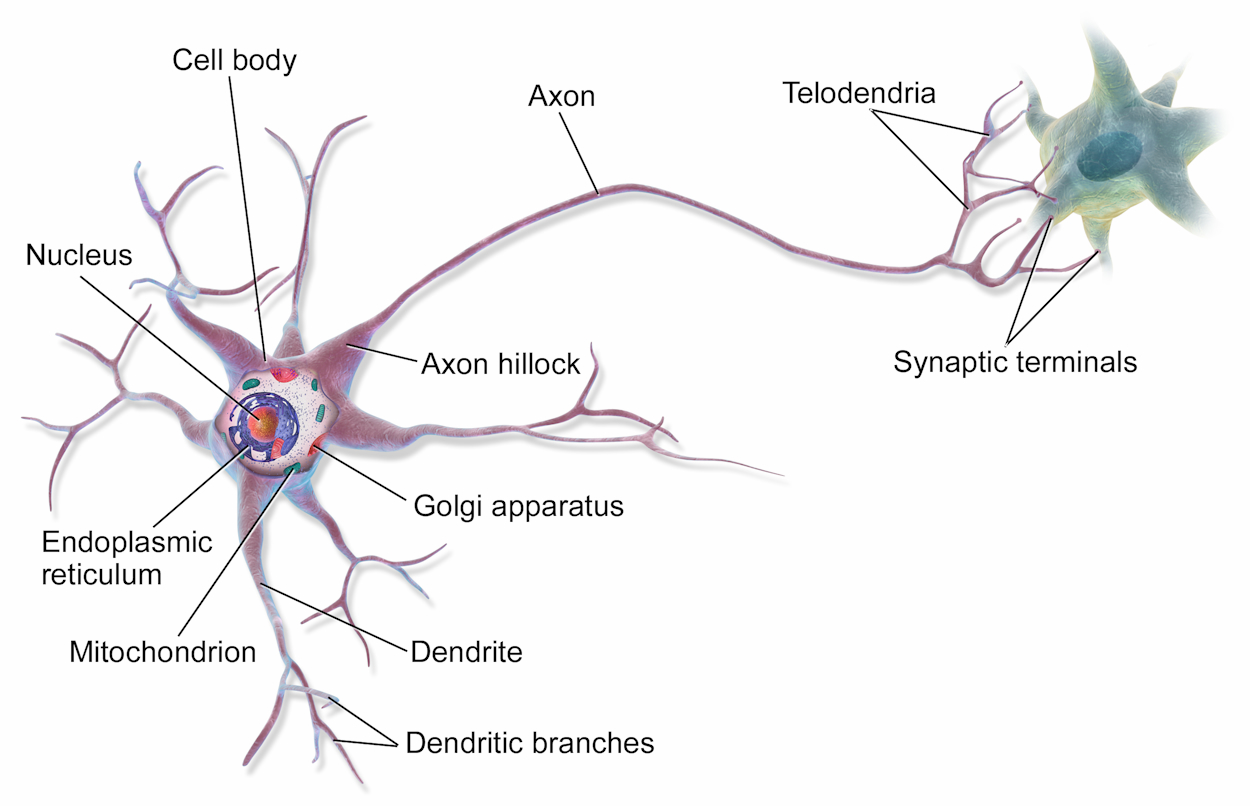
以上都是大家在生物课本上看到过的,
接下来是重点,我们来看看数学家们是怎么建模的
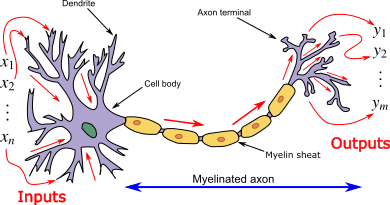
上图有太多的 x 和输入的 y,
我们首先来思考一个 x 输入和一个 y 输出的简单情况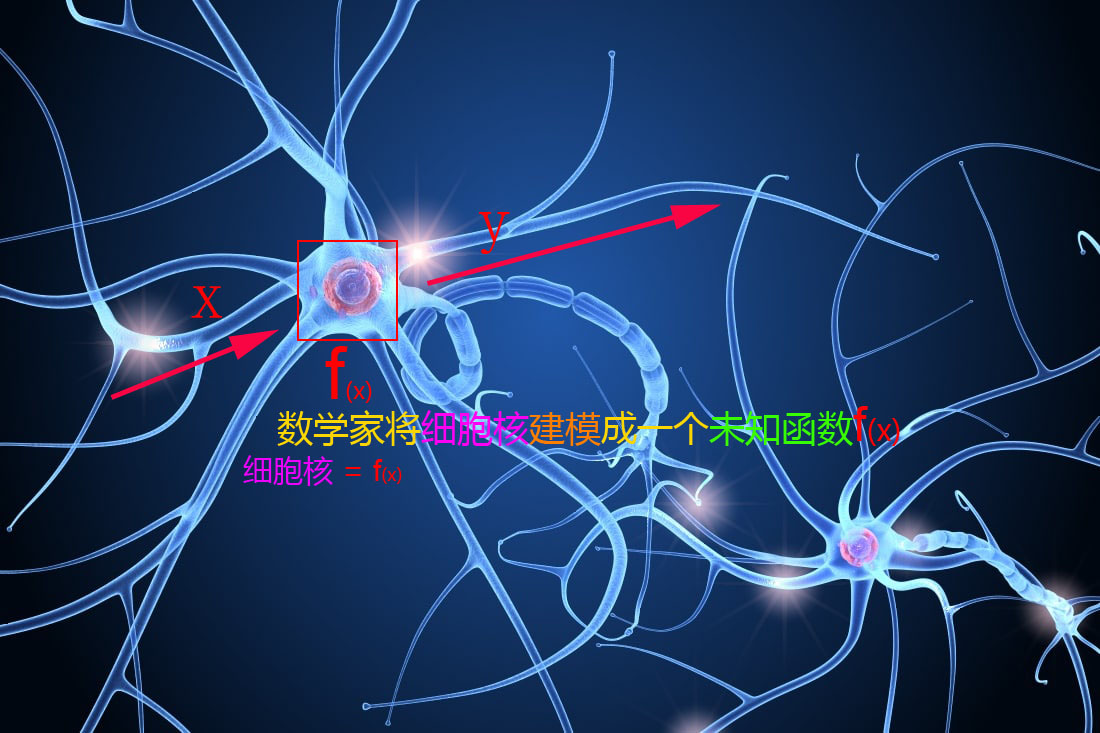
之所以,这样建模,是目前神经学家还不知道细胞核内是怎么运作的。
另外,细胞核所代表是函数 f 是怎么样的,并不是人一出生就固定的,
而是后天调节形成的!!
是后天调节形成的!!
是后天调节形成的!!
想象一下,你指着一只猫教一个孩子叫做“猫”,那么以后该孩子看到猫就会说是“猫”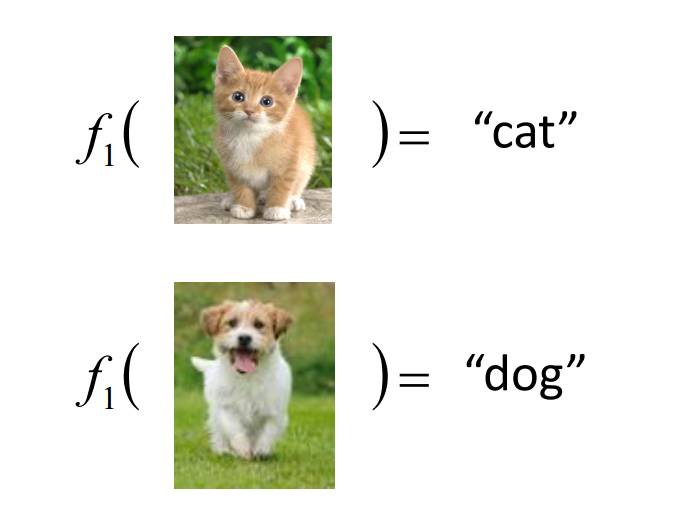
你指着一只猫教一个孩子叫做“猴子”,那么以后该孩子看到猫就会说是“猴子”
这里再用人的行为来解释一下:
在古代,普通人看到英国王族,那么就会下意识地下跪,
看到 英国王族(输入) → 下跪(输出)
但现代的人看到英国王族,下意识的反应会合照,签名,发朋友圈三连。
看到 英国王族(输入) → 合照,签名,发朋友圈(输出)
同应的输入,但经过不同训练后神经细胞则会得到不同的答案。
我们用数学来模拟这个调节过程,由于细胞核可以代表任意 f,
那么我们就用最简单的函数表述就好了~
已知方程 y=kx+b,当 x=6 时,y=15,求k,b的值。
| x | 假设方程 | 假设方程值(预测值) | 真实值 | 评估 |
|---|---|---|---|---|
| 6 | _y=1x+1 | _y=7 | y=15 | 预测值与真实值 相差甚远 |
| 6 | _y=2x+2 | _y=14 | y=15 | 预测值与真实值 很接近了 |
| 6 | _y=3x+3 | _y=21 | y=15 | 预测值与真实值 超过了 |
| 6 | _y=2.1x+2.3 | _y=14.9 | y=15 | 预测值与真实值 超接近了 |
于是大概解得:k=2.1,b=2.3,也就是函数是: y=2.1x+2.3;
上面说了,当 x=6 时,y=15,我们将 6 函数 y=2.1x+2.3,
得 2.1x6+2.3 = 14.9, 但与 15 不匹配,那是因为这个建模还没完成…
我们看回图,信息经过细胞核后,还要经过一段很长的 Axon(轴突)
在人工智能中是用权重或激活函数来代表 Axon(轴突),但这里我们用经验这个词,
于是得下面
| x | 假设方程和值 | 经验(四舍五入) | 理想方程和值 | 是否匹配 |
|---|---|---|---|---|
| 4 | 2.1x+2.3=10.7 | 10.7 → 11 | 2x+3=11 | √ |
| 5 | 2.1x+2.3=12.8 | 12.8 → 13 | 2x+3=13 | √ |
| 6 | 2.1x+2.3=14.9 | 14.9 → 15 | 2x+3=15 | √ |
| 7 | 2.1x+2.3=17 | 17 → 17 | 2x+3=17 | √ |
| 8 | 2.1x+2.3=19.1 | 19.1 → 19 | 2x+3=19 | √ |
| 9 | 2.1x+2.3=21.2 | 21.2 → 21 | 2x+3=21 | √ |
| 50 | 2.1x+2.3=107.3 | 107.3 → 107 | 2x+3=103 | x |
为什么需要经验,下章讲,这里留坑
我们已经对一个脑细胞进行建模,那么大脑又应该怎么建模呢?

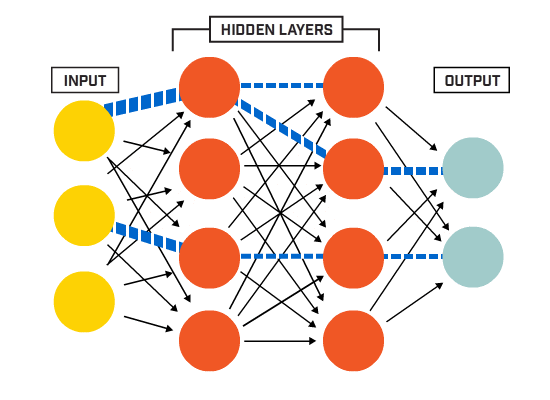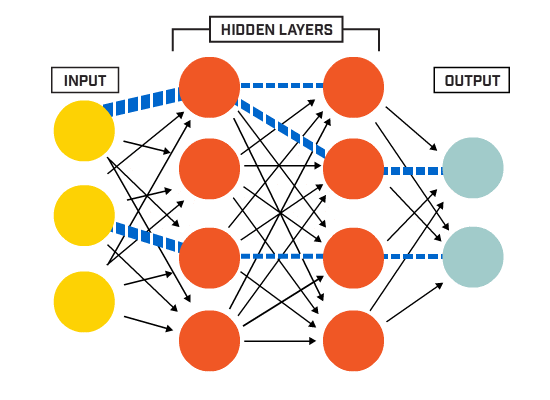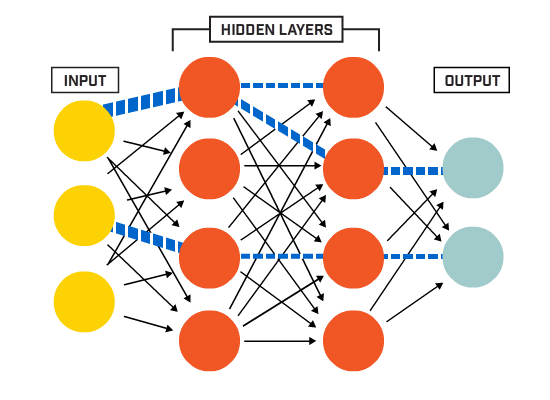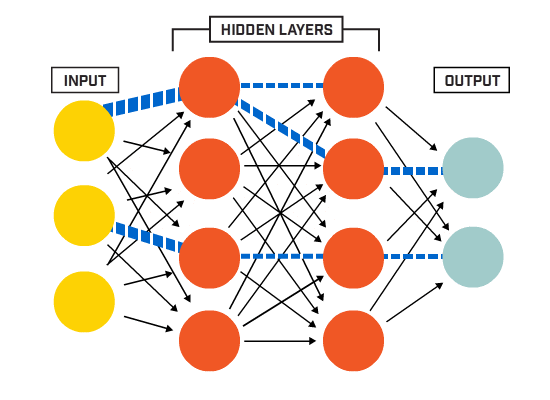
一个函数是:y=kx+b
那么一组函数就可以表示成如下图所示: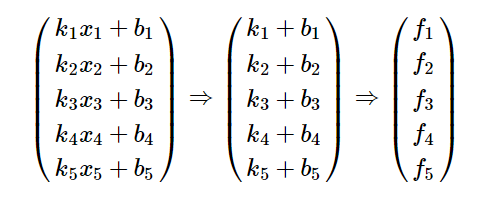
然后由于我们的大脑的网络神经是一个连接一个,也就是多层的,所以就如下图所示:
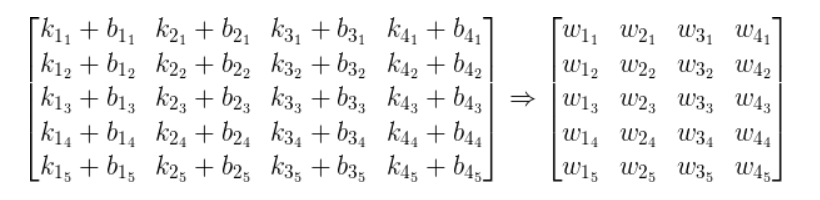
然后 w11 到 w45 都有比较适当(注意,是适当)的值,那么就是一个不错的人工智能了。
为什么是适当的值,而不是像初中求解方程(函数)那样如消元法,得到正确的方程(函数)?
假设我们在一张 28像素 28像素 上面写一个数字,要人工智能判断我们写的数字是多少?
我们需要先构造一个矩阵,然后将 `2828=784个x` 作为输入值传给这个矩阵(人工智能),
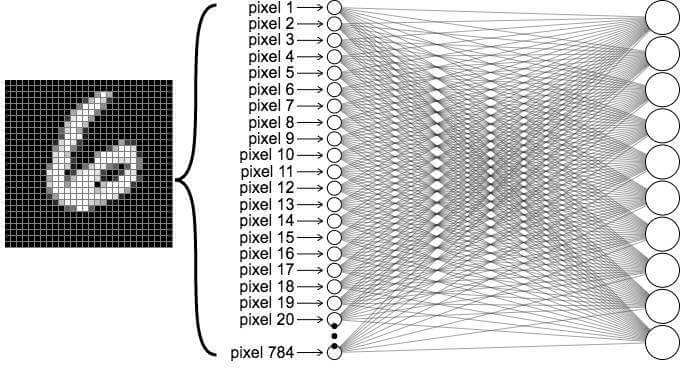
我们的眼睛至少是 1000像素 级别的,所以我们随便扫看一下,最少有1000*1000=1百万 个 x 作为输入值传给我们的大脑,而我们的大脑有 860亿 个神经细胞,也就是有 860亿 个方程(函数),消元是不可能消元的,这辈子都不可能消元;调节,如同进化论,适应者生存。
观看下图,感受一下什么叫调节,数字是会变动的: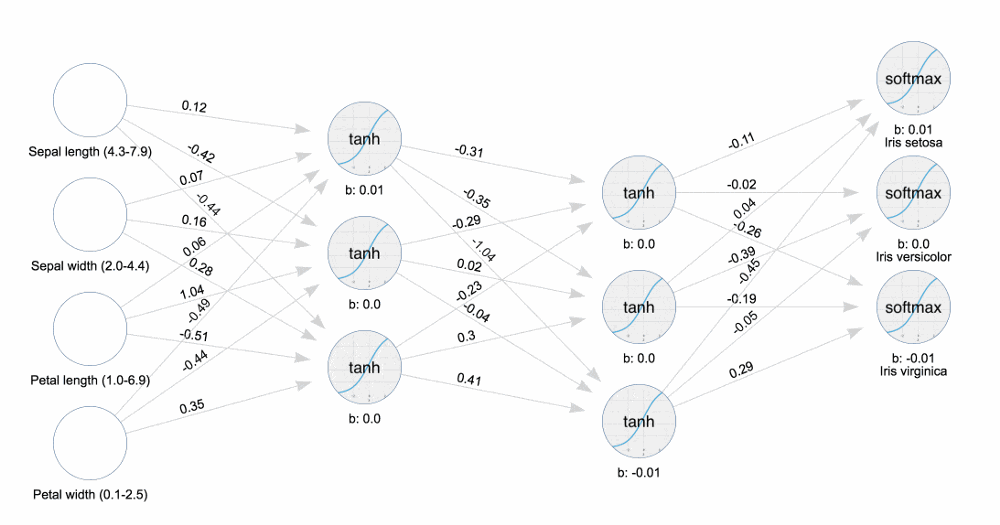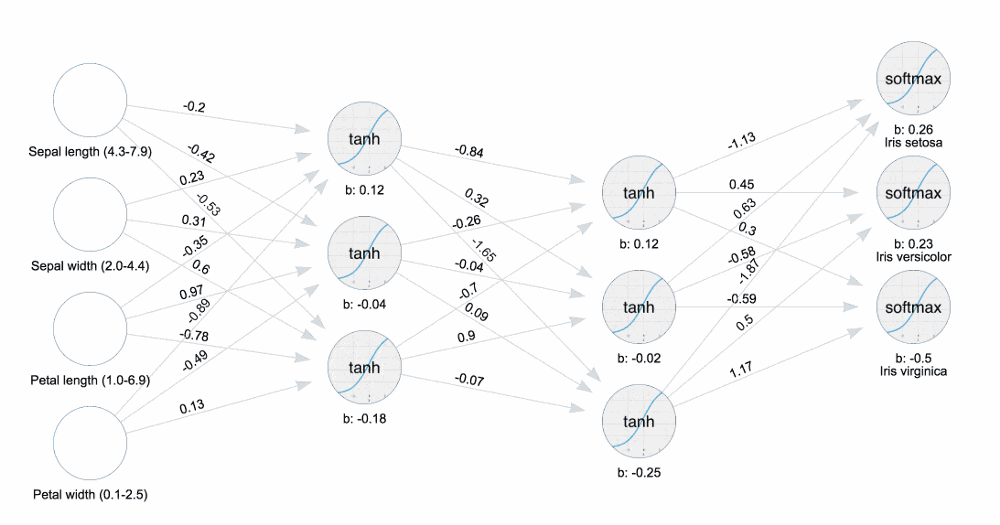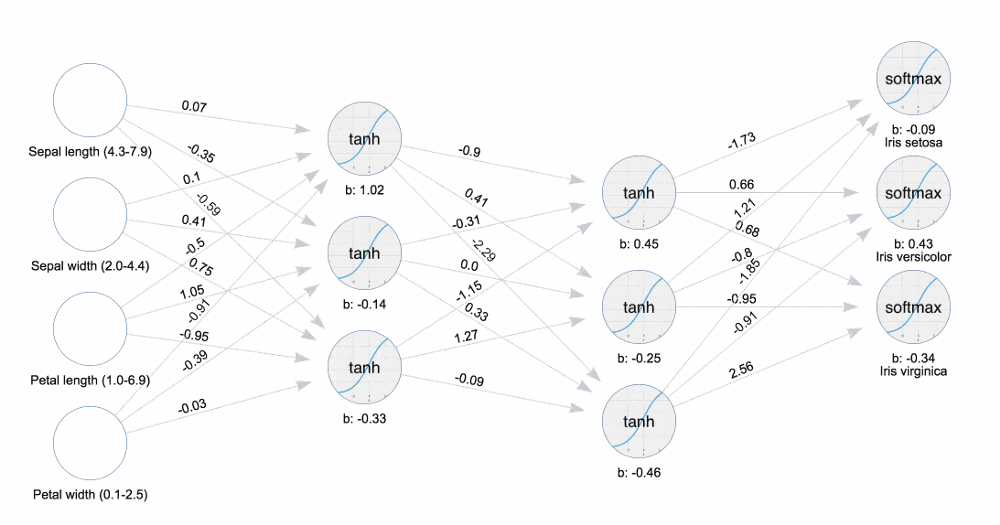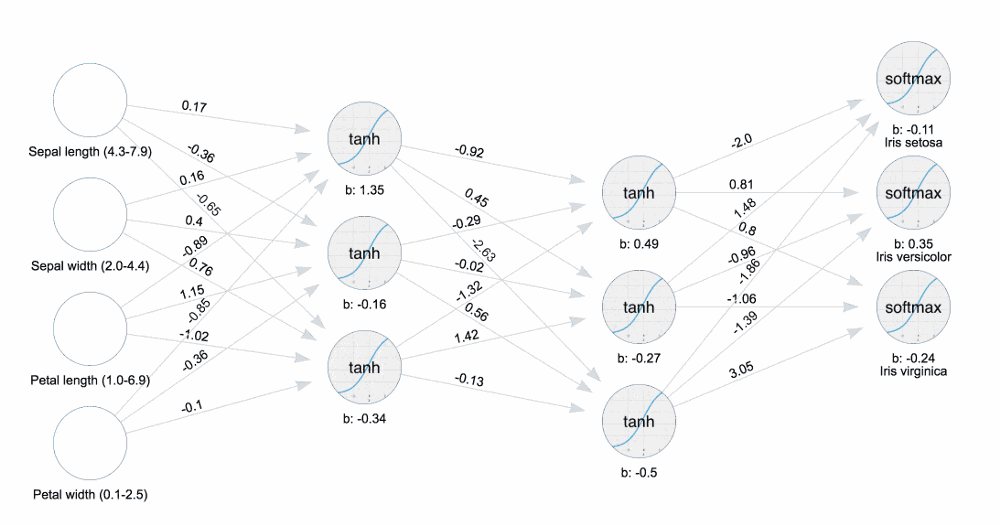
人工智能如此简单
第一步:创造人工智能(假设图片识别)
- 怎么创造?定义人工智能的大脑
- 怎么定义?用神经网络
- 怎么描述神经网络?用矩阵
第二步:训练人工智能
- 怎么训练?提供(图片)材料让人工智能训练
- 目的?让矩阵有适当的值,和适当的经验
总结与展望
没有研究生以上的数学知识的确没有机会去创造人工智能,让我们将注意力放在生物学家对大脑的研究上,了解我们的大脑是怎么运作的,还有,每个人都会为人父母,也就是说,你将会创造出史上最强的“智能”,那么接下来,你将会怎么训练呢????
下一章将解释机器训练——对应大脑在学习过程中的变化,看看神经学家们发现了什么,数学家们又是如何建模。
或许你会找到聪明的定义,何为聪明。
目前人工智能应用最好的是翻译,所以你也许能找到学习外语的最好方式~

